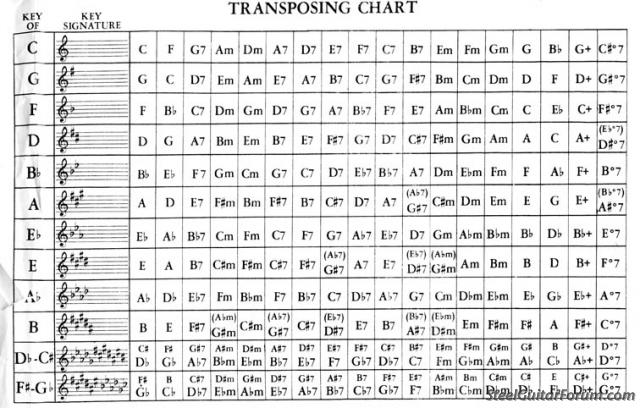
Transposing Chart

[Andy Volk]

There was a question on the lap steel forum about transposing chords from one key to another. While memorizing your music theory is indeed important, sometimes it's just easier just to see a quick reference and get on with it so here's a handy transposing chart that was lurking on my computer:

[Ellis Miller]

Andy, thank you for the excellent information.

Another suggestion is to learn to chart and read numbers which eliminates the need for detailed transposition.

[b0b]

I understand that the rows are ordered
all natural
1 sharp
1 flat
2 sharps
2 flats
etc.

but I don't follow the ordering of the columns at all. Is it just selection of chords that one might find in the given key signature, in random order?

I never knew that transposing was so complicated! I could never memorize a chart like that.

[Dave Mudgett]

I don't think it needs to be that complicated. If I was going to memorize it, I'd do it in cycle-of-fifths along one axis, and cycle-of-fourths on the other:

[tab]
Toeplitz-Structure Cycle-of-Fifths vs Cycle-of-Fourths Chord Transposition Matrix[sup]©[/sup]:

Key/Chord 1 5 2 6 3 7 5b b2 b6 b3 b7 4 1

C C G D A E B Gb Db Ab Eb Bb F C

F F C G D A E B Gb Db Ab Eb Bb F

Bb Bb F C G D A E B Gb Db Ab Eb Bb

Eb Eb Bb F C G D A E B Gb Db Ab Eb

Ab Ab Eb Bb F C G D A E B Gb Db Ab

Db/C# Db Ab Eb Bb F C G D A E B Gb Db

Gb/F# Gb Db Ab Eb Bb F C G D A E B Gb

B B Gb Db Ab Eb Bb F C G D A E B

E E B Gb Db Ab Eb Bb F C G D A E

A A E B Gb Db Ab Eb Bb F C G D A

D D A E B Gb Db Ab Eb Bb F C G D

G G D A E B Gb Db Ab Eb Bb F C G

C C G D A E B Gb Db Ab Eb Bb F C
[/tab]

This gives a Toeplitz matrix structure, with the same chord down each diagonal in the matrix. If you go cycle-of-fourths (or fifths) on each axis, you get a Hankel matrix, with the same chord down each skew-diagonal. I visualize the Toeplitz form more easily, but that may be because I used Toeplitz matrices in my system theory work for a long time. But this does give a very simple structure that displays the symmetry well. Note that this method also groups the flatted and sharped keys together in the matrix.

Similarly, if one goes up chromatically on one axis and down chromatically on the other axis, one gets the same type of Toeplitz structure. If one goes up or down chromatically (in the same direction) on each axis, then one again gets a Hankel form. For example, for the Hankel version, going up chromatically on each axis:

[tab]
Hankel-structure Chromatic-up vs. Chromatic-up Chord Transposition Matrix[sup]©[/sup]:

Key/Chord 1 b2 2 b3 3 4 b5 5 b6 6 b7 7 1

C C Db D Eb E F Gb G Ab A Bb B C

Db Db D Eb E F Gb G Ab A Bb B C Db

D D Eb E F Gb G Ab A Bb B C Db D

Eb Eb E F Gb G Ab A Bb B C Db D Eb

E E F Gb G Ab A Bb B C Db D Eb E

F F Gb G Ab A Bb B C Db D Eb E F

Gb Gb G Ab A Bb B C Db D Eb E F Gb

G G Ab A Bb B C Db D Eb E F Gb G

Ab Ab A Bb B C Db D Eb E F Gb G Ab

A A Bb B C Db D Eb E F Gb G Ab A

Bb Bb B C Db D Eb E F Gb G Ab A Bb

B B C Db D Eb E F Gb G Ab A Bb B

C C Db D Eb E F Gb G Ab A Bb B C
[/tab]

You get a Toeplitz or Hankel matrix like this whenever maintaining symmetry or antisymmetry along the axes. The chord flavor (major vs. minor vs maj7 vs b7 and so on) is not critical, since it is invariant along each column. I find that first cycle-of-fifths vs cycle-of-fourths type of format much easier to visualize, over the chromatic or other type of structure.

Actually, I've never seen it written this way, or discussed as a Toeplitz or Hankel matrix - it may be out there, but I've never seen it. That's why I'm putting a copyright mark on it - otherwise, this becomes strictly public-domain according to forum rules. It's not that it's a big deal - I just expect that if someone (like an academic) uses it in their writings, they acknowledge the source, rather than claim it as their own. I am, of course, curious if someone has written about this earlier.

I noticed some of these forms while using transposition matrices like this to compute chord synonyms several years back. I was mainly using the chromatic Toeplitz form most of the time.

[b0b]

The second one (Hankel) is the way I always think of it. I didn't know it had a name.

[Scott Shipley]

The Nashville Number System is much easier.

[Dave Mudgett]

The second one (Hankel) is the way I always think of it. I didn't know it had a name.

Yup, probably most people would order the notes on each axis in the same direction, which gives a Hankel matrix.

The Nashville Number System is much easier.

Oh, I definitely prefer numbers most of the time. Each row of that chromatic Hankel form shows the obvious and direct correspondence to the number system in the obvious way.

But there are other ways to look at it. I like the first form (cycle of fourths/fifths) because it clearly shows the symmetry of chord transpositions and key signatures at the same time. I'll bet that really good music readers understand this intuitively.

Note that for any Toeplitz or Hankel matrix, one only needs to memorize one row, because all the other rows are just cyclically-shifted versions of the first one. For a Toeplitz matrix, successive rows cyclically shift one position to the right - for a Hankel, to the left.